|
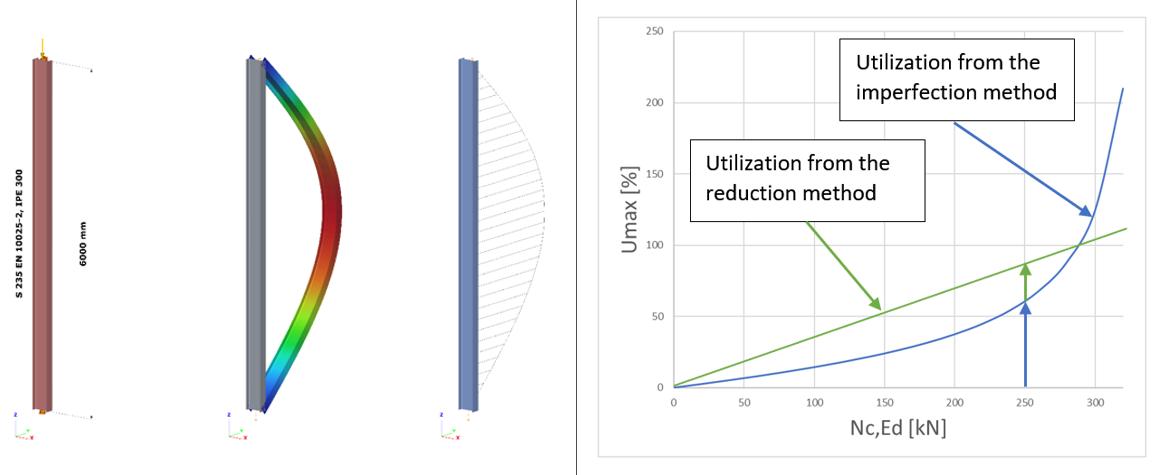
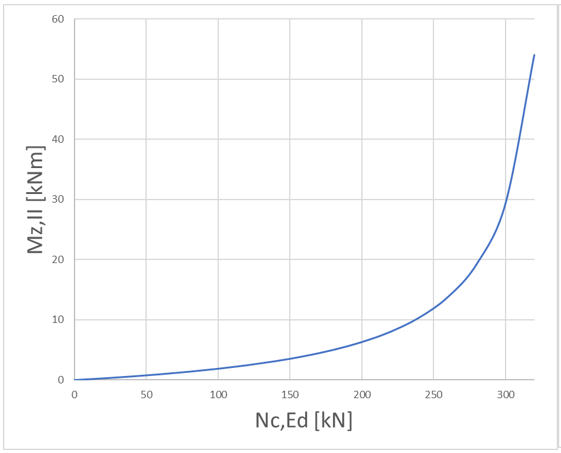
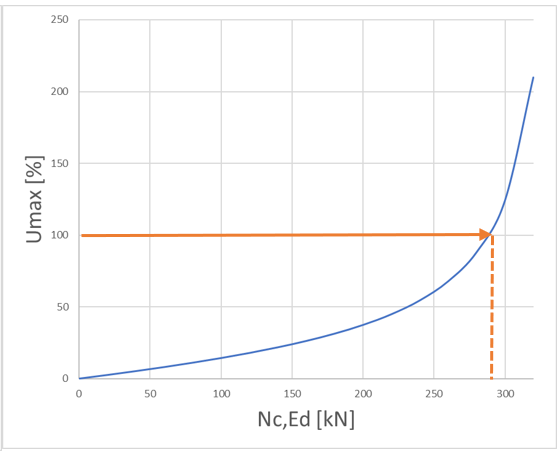
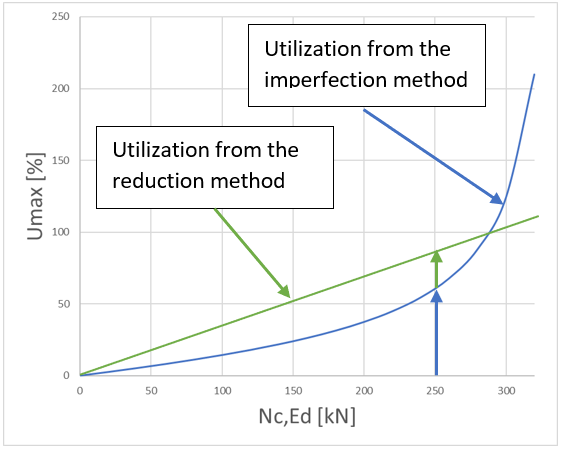
Μέρος 1. Διαφορές αντοχής μεταλλικών διατομών σε λυγισμό Ο Ευρωκώδικας EN 1993-1-1 προσφέρει βασικά δύο μεθόδους για την επαλήθευση της αντοχής των μελών: (1) βάσει συντελεστών μείωσης λυγισμού (καμπύλες λυγισμού) και (2) με βάση ισοδύναμες γεωμετρικές ατέλειες. Αυτό το μέρος εξετάζει τον τρόπο με τον οποίο οι δύο αυτές μέθοδοι σχετίζονται μεταξύ τους όσον αφορά την τελική χρήση των μελών. Για λόγους απλότητας, θεωρούμε ότι τα μέλη υποβάλλονται μόνο σε καθαρή θλίψη ή καθαρή κάμψη, υφίστανται κάμψη με ροπή ή πλευρική στρέψη. Για την περίπτωση (1) χρησιμοποιούνται τα κεφάλαια 6.3.1 και 6.3.2 ενώ για την περίπτωση (2) οι ατέλειες θεωρούνται ότι έχουν συγκεκριμένη μορφή λυγισμού και το βασικό κεφάλαιο είναι το 5.3.2 (11). Είναι προφανές ότι αυτές οι δύο τυπικές διαδικασίες πρέπει να αποφέρουν την ίδια απόδοση σε ένα μέλος από τη στιγμή που οι εντάσεις είναι ίδιες. Ωστόσο, αυτό γενικότερα δε συμβαίνει. Ας δούμε το ακόλουθο απλό παράδειγμα ενός απλά υποστηριζόμενου, θλιβόμενου υποστυλώματος με διατομή κατηγορίας 2 (επιτρέπεται υπολογισμός πλαστικής αντίστασης). Το υποστύλωμα έχει ύψος 6 μέτρων και έχει διατομή IPE300 από χάλυβα S235. Το πρότυπο πλάτος για την ατέλεια βασισμένο στην μορφή λυγισμού υπολογίζεται από την εξίσωση. 5.9-5.11, που είναι ίση με v0 = 13.4 mm. Το επόμενο σχήμα δείχνει το μοντέλο, την μορφή λυγισμού το οποίο αποτελεί κλασσική περίπτωση καμπτικού λυγισμού γύρω από τον ασθενή άξονα - και τη κατανομή της ροπής του δεύτερου κατά σειρά ασθενούς άξονα. Εδώ αξίζει να σημειωθεί ότι η επαλήθευση που βασίζεται στην μέθοδο της ισοδύναμης γεωμετρικής ατέλειας πρέπει να υπολογιστεί από τα αποτελέσματα μιας ανάλυσης δευτέρας τάξεως χρησιμοποιώντας τον έλεγχο μιας ραβδωτής διατομής όπως ορίζεται από την εξίσωση. 6.2 (ή εξίσωση 6.1 ισχύει για ελαστικές περιπτώσεις). Σχήμα 1. Θλιβόμενο υποστύλωμα , Παραμόρφωση λόγω λυγισμού και η κατανομή της ροπής κάμψης από ανάλυση δευτέρας τάξεως λόγω των ατελειών Η κρίσιμη διατομή είναι η μεσαία, όπου η τιμή ροπής κάμψης δεύτερης τάξης εξαρτάται φυσικά από το επίπεδο της θλιπτικής δύναμης σύμφωνα με τη γνωστή σχέση : όπου Nc, Ed είναι η εφαρμοζόμενη δύναμη θλίψης, v0 είναι το εύρος της ισοδύναμης γεωμετρικής ατέλειας και είναι ο συντελεστής ενίσχυσης που εξαρτάται από το ελαστικό κρίσιμο φορτίο N.cr = 347,6 kN (φορτίο Euler). Η χρησιμοποίηση αυτής της κρίσιμης διατομής μπορεί να υπολογιστεί σύμφωνα με την εξίσωση. (6.2): Το σχήμα 2 δείχνει τη σχέση μεταξύ της εφαρμοζόμενης θλιπτικής δύναμης, της ροπής κάμψης δεύτερης τάξης και της χρήσης της μεσαίας διατομής όπου το N.Rd = 1264,6 kN και το MzRd = 29,28 kNm. Η απόδοση/αντοχή της διατομής εξαρτάται μη γραμμικά από το επίπεδο της θλιπτικής δύναμης λόγω της μη γραμμικότητας της ροπής κάμψης δεύτερης τάξης. Η απόδοση που αντιστοιχεί στην τιμή 100% δίνει την αντίσταση του υποστυλώματος στο λυγισμό: Σχήμα 2. Η κάμψη δεύτερης τάξης και η απόδοση του υποστυλώματος Η αντίσταση στο λυγισμό μπορεί επίσης να υπολογιστεί με τη μέθοδο του συντελεστή μείωσης χρησιμοποιώντας τις εξισώσεις. 6.46-6.49: Παρέχει τα ίδια αποτελέσματα με αυτά που υπολογίζονται με την μέθοδο ισοδύναμων ατελειών, πράγμα που σημαίνει ότι οι δύο μέθοδοι, μέσω των σχέσεων 5.9-5.11 και 6.46-6.49 είναι συνεπείς όσον αφορά την τιμή αντίστασης στο λυγισμό. Εντούτοις, η απόδοση του λυγισμού του υποστυλώματος μπορεί να υπολογιστεί από την κοινή γραμμική σχέση της Εξ. 6.46: Στο Σχήμα 3, απεικονίζονται οι δύο τιμές απόδοσης. Παρατηρείται εδώ, ότι οι δύο αποδόσεις είναι ίσες στο επίπεδο/σημείο του φορτίου αντοχής στο λυγισμό. Όταν η εφαρμοζόμενη θλιπτική δύναμη είναι μικρή, η μέθοδος συντελεστή μείωσης δίνει μεγαλύτερη απόδοση, ενώ όταν η εφαρμοζόμενη θλιπτική δύναμη είναι υψηλή, η μέθοδος ατελειών δίνει μεγαλύτερη απόδοση. Σχήμα 3. Απόδοση της μεθόδους μειωτικών συντελεστών και της μεθόδου των ατελειών Η διαφορά οφείλεται σαφώς στη μη γραμμικότητα της μεθόδου ατελειών. Για παράδειγμα, αν η εφαρμοζόμενη δύναμη θλίψης είναι NcEd = 250 kN οι τιμές απόδοσης εμφανίζουν σημαντική διαφορά (βλ. Σχήμα 3): Μπορεί γενικά να δηλωθεί ότι η μέθοδος των ατελειών αντιπροσωπεύουν την "αληθινή" (μη γραμμική) χρήση, ενώ η μέθοδος των συντελεστών δείχνουν την ακριβή απόδοση μόνο στην αντίσταση στο λυγισμό. Για την επάρκεια του μέλους, ωστόσο, και οι δύο μέθοδοι είναι σωστές.
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
ERGOCADΝέα και ενδιαφέροντα άρθρα, tips, events κ.α. ΑΡΧΕΙΟ
May 2024
ΚΑΤΗΓΟΡΙΕΣ
All
|

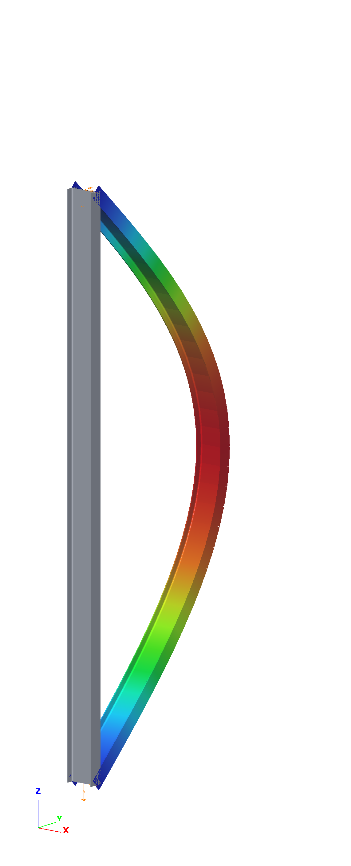

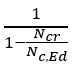
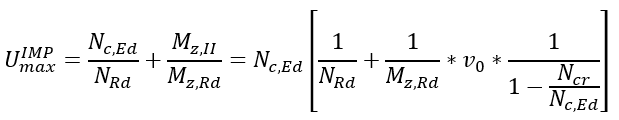
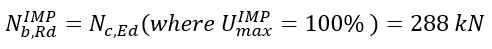
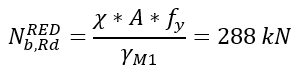
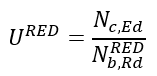
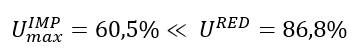
 RSS Feed
RSS Feed