Γραμμικό άθροισμα συνδυασμών των μορφών ταλάντωση ως εναλλακτικός τρόπος αντί για την μέθοδο CQC

Η πιο συχνά εφαρμοζόμενη προσέγγιση για τον προσδιορισμό της σεισμικής επίδρασης για την οποία πρέπει να σχεδιαστεί μια κατασκευή είναι η Ανάλυση με το Φάσμα Απόκρισης (MRSA). Αυτή η προσέγγιση βασίζεται στην εκχώρηση κατάλληλων επιταχύνσεων στις διάφορες μορφές ταλάντωσης μιας κατασκευής, με βάση μια συνάρτηση που ονομάζεται φάσμα και ορίζει τις μέγιστες αναμενόμενες επιταχύνσεις σε συνάρτηση με τις περιόδους ταλάντωσης.
Εφόσον η δυναμική απόκριση μιας κατασκευής μπορεί να προσεγγιστεί από την απόκριση ενός προβόλου με μία μόνο μάζα, η κατάσταση είναι απλή, η κατασκευή μπορεί να περιγραφεί με μία μοναδική ιδιομορφή ταλάντωσης και κατά συνέπεια το MRSA οδηγεί σε μία μόνο δύναμη.
Όταν η κατασκευή γίνει πιο περίπλοκη και η συγκέντρωση των μαζών της σε ένα μόνο σημείο δεν είναι πια δυνατή, πρέπει να αντιμετωπιστεί ως ένα σύστημα πολλαπλών μαζών το οποίο όμως έχει πολλούς τρόπους ταλάντωσης. Για το λόγο αυτό υπάρχει μία διαδικασία που βασίζεται σε διάφορες μεθόδους υπολογισμών. Στο παρόν άρθρο παρακάτω παρουσιάζονται οι αδυναμίες των μεθόδων αυτών καθώς και μία εναλλακτική μέθοδος που εφαρμόζεται στο Consteel.

Το άρθρο αυτό παρουσιάστηκε κατά τη διάρκεια του 5ου Πανελλήνιου Συνεδρίου Αντισεισμικής μηχανικής τεχνικής σεισμολογίας, 20-22 Οκτώβρη 2022, στην Αθήνα, στο οποίο η ERGOCAD ήταν επίσημος υποστηρικτής (βλ. εικόνες που ακολουθούν). 

​Εφόσον μια κατασκευή έχει συμμετρική κατανομή μάζας και ακαμψίας χωρίς απότομες αλλαγές, ακόμη και αν είναι σύστημα πολλαπλών μαζών, η δυναμική της συμπεριφορά μπορεί να περιγραφεί επαρκώς από μία μορφή ταλάντωσης, η οποία χαρακτηρίζεται συνήθως από την πρώτη ιδιομορφή. Η συνάφεια μιας δεδομένης μορφής ταλάντωσης συνήθως χαρακτηρίζεται από τον συντελεστή σχετικότητας μάζας. Εάν η σχετικότητα μάζας μιας μεμονωμένης μορφής είναι πολύ υψηλή σε σύγκριση με άλλες ιδιομορφές αυτή η μορφή ταλάντωσης ονομάζεται κυρίαρχη λειτουργία.

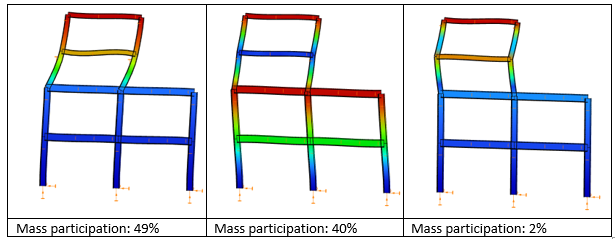
​Μια κατασκευή με κυρίαρχη ιδιομορφή μπορεί να αντιμετωπιστεί τυπικά ως κατασκευή μιας μάζας, αλλά με μάζες συγκεντρωμένες σε διαφορετικά σημεία και όλες αυτές οι μάζες πολλαπλασιάζονται με μία μόνο επιτάχυνση που αντιστοιχεί στην κυρίαρχη μορφή ταλάντωσης. Το σύνολο δυνάμεων που προκύπτει θεωρείται ότι είναι ισοδύναμο με το σεισμικό αποτέλεσμα που επενεργεί σε αυτή τη κατασκευή.
Όταν μια κατασκευή γίνει πιο περίπλοκη, δεν θα είναι δυνατή η επιλογή μιας μόνο ιδιομορφής ταλάντωσης για να περιγραφεί η δυναμική συμπεριφορά της και θα πρέπει επίσης να ληφθούν υπόψη περαιτέρω μορφές ταλάντωσης.
Εάν περισσότερες από μία ιδιομορφές ταλάντωσης είναι σχετικές, το MRSA θα παρέχει για καθεμία από αυτές τις διαφορετικές ιδιομορφές μια αντίστοιχη επιτάχυνση. Η κατασκευή θα πρέπει να σχεδιαστεί για την ταυτόχρονη επίδραση των διαφορετικών επιταχύνσεων που αντιστοιχούν στις περιόδους ταλάντωσης των διαφορετικών ιδιομορφών ταλάντωσης. Οι δυνάμεις που υπολογίζονται από το MRSA για κάθε διαφορετικό τρόπο ταλάντωσης δεν μπορούν απλώς να προστεθούν γιατί αυτό θα δημιουργούσε ένα αδικαιολόγητα υψηλό αποτέλεσμα.
Αντί για μια απλή άθροιση των επιμέρους δυνάμεων που λαμβάνονται για διαφορετικούς τρόπους ταλάντωσης, προτείνεται μια πιο περίπλοκη λύση στους περισσότερους σύγχρονους σεισμικούς κώδικες που χρησιμοποιεί έναν τετραγωνικό κανόνα, που ονομάζεται SRSS ή CQC.

​Αυτές οι μέθοδοι είναι στατιστικές και στόχος τους είναι η παροχή μιας αναμενόμενης μέγιστης τιμής της εν λόγω εσωτερικής δύναμης ή συνιστώσας παραμόρφωσης. Για να συμβεί αυτό, πρέπει πρώτα να υπολογιστούν στην κατασκευή οι συνιστώσες της εσωτερικής δύναμης και παραμόρφωσης για τις δυνάμεις κάθε διαφορετικού τρόπου ταλάντωσης χρησιμοποιώντας μια γραμμική στατική ανάλυση (LA).
Η αναμενόμενη «συνολική» τιμή της μετατόπισης της συνιστώσας εσωτερικής δύναμης σε ένα σημείο της κατασκευής μπορεί να ληφθεί με την εφαρμογή της μεθόδου SRSS ή CQC στις ίδιες τιμές διαθέσιμες για κάθε μορφή ταλάντωσης ξεχωριστά, ως αποτέλεσμα του LA. Οι μέγιστες τιμές που προκύπτουν μπορούν να χρησιμοποιηθούν χωρίς προβλήματα για την εκτέλεση των ελέγχων αντοχής διατομής ή της εκτίμησης της μέγιστης τιμής μετατόπισης. Είναι σημαντικό να σημειωθεί, ότι λόγω της χρήσης ενός μη γραμμικού τετραγωνικού συνδυασμού, δεν είναι δυνατή μια ισοδύναμη περίπτωση μονής φόρτισης που να έχει την ίδια εσωτερική δύναμη και συνιστώσες μετατόπισης σε κάθε σημείο της κατασκευής ταυτόχρονα.

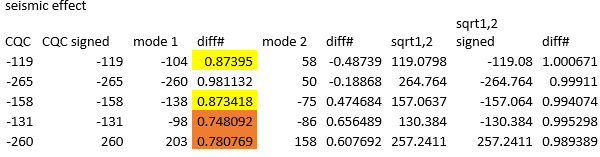
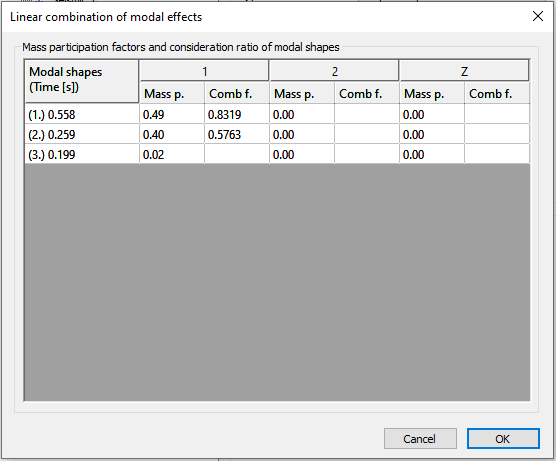
​Αυτή η διαδικασία όμως έχει διάφορες συνέπειες:
• Οι τιμές χάνουν το αρχικό τους πρόσημο, καθώς η λογική του τετραγωνικού αθροίσματος θα παράγει πάντα θετικά αποτελέσματα.
• Καθώς οι τιμές που λαμβάνονται σε κάθε διαφορετικό σημείο της κατασκευής δεν αντιστοιχούν στο ίδιο σύνολο φορτίων, δεν υπάρχει εγγύηση ότι οι δυνάμεις που λαμβάνονται κοντά σε μια σύνδεση με πολλά συνδεδεμένα μέλη βρίσκονται σε ισορροπία. Οι προκύπτουσες δυνάμεις που λαμβάνονται από μέλη που ενώνονται σε έναν κόμβο δεν μπορούν να χρησιμοποιηθούν απλώς ως δεδομένα για τους σκοπούς σχεδιασμού σύνδεσης.
• Δεν υπάρχει καμία εγγύηση ότι οι γνωστές σχέσεις μεταξύ των τιμών της διατμητικής δύναμης και των ροπών κάμψης που προκύπτουν αντικατοπτρίζονται στα «συνοπτικά» μεγέθη. Επομένως, οι γνωστοί τύποι αλληλεπίδρασης που βασίζονται σε αυτή τη σχέση δεν είναι εφαρμόσιμοι
• Για τον ίδιο λόγο, η κατανομή των εσωτερικών δυνάμεων κατά μήκος ενός μέλους δεν αντιστοιχεί απαραίτητα στην ίδια επίδραση φορτίου και επομένως οποιαδήποτε μέθοδος που θα εξάγει συμπεράσματα με βάση την πραγματική τους κατανομή δεν είναι εφαρμόσιμη
• Καθώς η σεισμική επίδραση δεν μπορεί να περιγραφεί από ένα ισοδύναμο σύστημα φορτίου, η γνωστή γεωμετρική ανάλυση δεύτερης τάξης (GNA) δεν μπορεί να εφαρμοστεί στην κατασκευή
• Για τον ίδιο λόγο δεν μπορεί να πραγματοποιηθεί ανάλυση γραμμικού λυγισμού (LBA) για τη λήψη σημαντικών γενικών πληροφοριών λυγισμού της κατασκευής.

​Πρόταση για χρήση γραμμικών συνδυασμών των ιδιομορφών
Εάν μπορούσε να καθοριστεί ένα ισοδύναμο σύνολο δυνάμεων, κανένα από τα προβλήματα που αναφέρθηκαν παραπάνω δεν θα συνέβαινε στην περίπτωση των πολύπλοκων κατασκευών. Για μια κατασκευή συνήθως υπάρχει μία κυρίαρχη μορφή ταλάντωσης και θα υπάρχουν αρκετές άλλες των οποίων η συμβολή θα λαμβάνεται επίσης υπόψη. Σε περίπτωση σύνθετης κατασκευής, ενδέχεται να υπάρχουν τμήματα της κατασκευής (υποκατασκευές), για τα οποία η κυρίαρχη ιδιομορφή είναι διαφορετική από τη συνολική κυρίαρχη ιδιομορφή λαμβάνοντας υπόψη ολόκληρη τη κατασκευή. Ο στόχος εδώ είναι να βρεθεί λοιπόν η κυρίαρχη ιδιομορφή και όσες άλλες συνεισφέρουν ώστε να προετοιμαστούν οι κατάλληλοι γραμμικοί συνδυασμοί που θα μπορούν να χρησιμοποιηθούν, για να υπολογιστούν τα αθροίσματα των τιμών. Για να βρεθεί η λύση στο πρόβλημα των υποκατασκευών, ο στόχος δεν είναι να δημιουργηθεί ένα μόνο ισοδύναμο φορτίο αλλά πολλά, συγκεντρωμένα σε εκείνο το τμήμα της κατασκευής όπου το καθολικό κυρίαρχο φορτίο έχει μικρότερη σχετικότητα και όπου άλλες τοπικές μορφές ταλάντωσης παίζουν σημαντικό ρόλο.

​Καθώς οι «συνολικές» τιμές που προκύπτουν από το άθροισμα των επιμέρους ιδιομορφών είναι σε κάθε σημείο οι μέγιστες τιμές που ορίζονται από τον εφαρμοσμένο κώδικα σχεδιασμού, αυτές θα αναγνωρίζονται ως τιμές αναφοράς. Στα ίδια σημεία της κατασκευής είναι επίσης διαθέσιμες οι τιμές που λαμβάνονται από κάθε ιδιομορφή ταλάντωσης. Οι γραμμικοί συνδυασμοί στοχεύουν σε αυτές τις τιμές αναφοράς. Για κάθε τέτοιο σημείο μπορεί να οριστεί μια εξίσωση και το σύστημα εξίσωσης που στοχεύει πολλά τέτοια σημεία αναφοράς. Αυτή θα μπορεί να γραφεί με την εξής μορφή:
Ax = b
​όπου
A είναι οι «τιμές» που λαμβάνονται για κάθε ξεχωριστή μορφή ταλάντωσης
b είναι οι «τιμές» αναφοράς
x είναι οι άγνωστοι πολλαπλασιαστές των μεμονωμένων ιδιομορφών που θα χρησιμοποιηθούν στον γραμμικό συνδυασμό
Η λέξη "τιμή" μπορεί να σημαίνει την επιθυμητή παραμόρφωση ή εσωτερική δύναμη.
Εάν ο αριθμός των σημείων αναφοράς είναι ίδιος με τον αριθμό των μορφών ταλάντωσης που θεωρούνται σχετικοί, το παραπάνω σύστημα εξισώσεων μπορεί απλά να λυθεί με
x = A-1 b

​Στην πράξη μπορεί να είναι επιθυμητό να δημιουργηθούν γραμμικοί συνδυασμοί που να έχουν ισχύ όχι μόνο για έναν μικρό αριθμό σημείων αναφοράς, αλλά και για μια ευρύτερη ζώνη γύρω από αυτά τα σημεία, ακόμα κι αν η αυτή η τιμή αποδεχτεί περισσότερο μία προσεγγιστική λύση παρά μία περιορισμένη αλλά ακριβής λύση . Σε αυτή την περίπτωση θα χρησιμοποιηθεί μεγαλύτερος αριθμός σημείων αναφοράς, με αποτέλεσμα ένα υπερκαθορισμένο σύστημα εξισώσεων. Αυτό το υπερκαθορισμένο σύστημα εξισώσεων μπορεί να λυθεί χρησιμοποιώντας τα κριτήρια ελαχίστου τετραγώνου, ελαχιστοποιώντας τη διαφορά μεταξύ του Ax και του b, που μετράται με το 2-norm.

​Σε οποιαδήποτε από τις περιπτώσεις, οι «τιμές» που προκύπτουν ως αποτέλεσμα του Ax θα χρησιμοποιηθούν αντί των τιμών αναφοράς (με τους δείκτες στα αντίστοιχα σημεία της κατασκευής) για το σημείο αναφοράς και επίσης για τα γειτονικά μέρη της κατασκευής. Το Ax είναι ένας γραμμικός συνδυασμός συνόλων δυνάμεων που λαμβάνονται από διαφορετικούς τρόπους ταλαντώσεων και ως εκ τούτου μπορεί να θεωρηθεί ως ένα μόνο ισοδύναμο φορτίο, αλλά με περιορισμένη εγκυρότητα που ορίζεται από την επιλογή των σημείων αναφοράς. Χρησιμοποιώντας αυτό το ισοδύναμο φορτίο αντί για τις "συνοπτικές" τιμές μπορούν να επιλυθούν όλα τα ζητήματα που αναφέρονται παραπάνω.

​Πιθανή ροή εργασίας με τις γραμμικά συνδυασμένες μορφές ταλάντωσης
Η ροή εργασίας παρουσιάζεται σε ένα απλό 2D πλαίσιο, χρησιμοποιώντας το λογισμικό Consteel. Το κάτω μέρος είναι πιο άκαμπτο από το πάνω μέρος. Αυτή είναι συνήθως μια κατάσταση όπου δεν μπορεί να βρεθεί μία μόνο κυρίαρχη μορφή με μια συνολική εγκυρότητα για ολόκληρη την κατασκευή.

Βήμα 1 
Εκτέλεση δυναμικής ανάλυσης της κατασκευής. Οι 3 πρώτες μορφές ταλάντωσης είναι οι εξής :
Mode 1 - f = 1.811 Hz, T = 0.562 sec 
Mode 2 - f = 3.85 Hz, T = 0.26 sec
Mode 3 - f = 5.021 Hz, T = 0.199 sec

Η συνολικά μάζα που ενεργοποιείται στις πρώτες 2 ιδιομορφές φτάνει στις ελάχιστες απαιτήσεις του Ευρωκώδικα 8, και επιπλέον η συνεισφορά της 3ης ιδιομορφής είναι εξαιρετικά χαμηλή, οπότε θα χρησιμοποιηθούν οι 2 πρώτες ιδιομορφές. Η κυρίαρχη ιδιομορφή για την κατασκευή είναι η 1, αλλά αναμένεται ότι αν λάβουμε υπόψη μόνο αυτή τα αποτελέσματα δεν θα είναι σωστά..

Βήμα 2
Πραγματοποιούμε εδώ μια ανάλυση MRSA και συγκρίνουμε  ακριβείς συνδυασμένες τιμές αναφοράς CQC με τα αποτελέσματα των ιδιομορφών. Σε αυτό το παράδειγμα μελετάμε μια σχεδίαση πλαισίου ροπής σύμφωνα με την κατηγορία πλαστιμότητας DCL και η κύρια εστίαση θα είναι η μέθοδος υπολογισμού των ροπών κάμψης που προκύπτουν από το σεισμικό φαινόμενο με γραμμικούς συνδυασμούς των ιδιομορφών. 

Αναφορά αποτελεσμάτων MRSA με τιμές αναφοράς, που θα χρησιμοποιηθούν για τη γραμμική μέθοδο. 
Οι σημειωμένες ακριβείς ροπές κάμψης που λαμβάνονται με το άθροισμα CQC θα θεωρηθούν ως τιμές αναφοράς (δείκτες στο σχήμα) και θα αποθηκευτούν στο διάνυσμα b

Βήμα 3
Ελέγχουμε τις κατανομές της ροπής κάμψης που αντιστοιχούν στον καθορισμένο αριθμό ιδιομορφών ταλάντωσης. 
Ιδιομορφή 1
Φαίνεται ότι χρησιμοποιώντας μόνο την πρώτη ιδιομορφή, δεν μπορεί να επιτευχθεί καλή συμφωνία με τις τιμές αναφοράς CQC. Για τη σύγκριση, τα πρόσημα των «συνοπτικών» τιμών CQC θα ρυθμιστούν όπως υπαγορεύεται από αυτή την πρώτη μορφή ταλάντωσης. Υπάρχει τέλεια συμφωνία λοιπόν σε ένα μόνο σημείο αναφοράς, στην κορυφή του πρώτου ορόφου της μικρότερης υποκατασκευής (264,57 - 260,14) που βρίσκεται στην κορυφή πιο άκαμπτης υποκατασκευής. Σε άλλο σημείο, ειδικά στο κάτω πιο άκαμπτο τμήμα η διαφορά είναι πολύ σημαντική, έως και 25%.

Ιδιομορφή 2
Σεισμική δράση

Η τελευταία στήλη δείχνει τις τιμές της ροπής κάμψης που υπολογίζονται σύμφωνα με μια απλή μέθοδο SRSS, λαμβάνοντας υπόψη τις δύο πρώτες ιδιομορφές. Όπως είναι ορατό, οι τιμές δείχνουν τέλεια συμφωνία με τις τιμές CQC που υπολογίζονται σε όλες τις διαθέσιμες ιδιομορφές. Αυτό επιβεβαιώνει ότι η εξέταση των δύο πρώτων τρόπων για τους συνδυασμούς τρόπων μπορεί να οδηγήσει σε επαρκή αποτελέσματα.

Βήμα 4
Κάνουμε μια πρώτη δοκιμή για να καλύψουμε με έναν μόνο γραμμικό συνδυασμό όλα τα επιλεγμένα σημεία αναφοράς. Τα διαθέσιμα αποτελέσματα οργανώνονται σε μορφή matrix, χρησιμοποιώντας τη σύνταξη του λογισμικού Matlab.

A = [-104 58; -260 50; -138 -75; -98 -86; 203 158]
  -104    58
  -260    50
  -138   -75
   -98   -86
   203   158
b = [-119; -265; -158; -131; 260]
  -119
  -265
  -158
  -131
   260
x = [x1; x2]

Το σύστημα των εξισώσεων Ax =b υπερκαθορίζεται στον πίνακα Α και έχει περισσότερες γραμμές από το διάνυσμα αγνώστων παραγόντων πολλαπλασιασμού. Για την επίλυσή του θα χρησιμοποιηθούν τα κριτήρια ελαχίστων τετραγώνων, χρησιμοποιώντας την ενσωματωμένη συνάρτηση Matlab
>> lsqr(A,B)
όπου το lsqr συγκλίνει στην επανάληψη 2 σε μία λύση με σχετική τιμή υπολοίπου ίση με 0.051.
ans =
     1.0923
    0.2118
Αυτό οδηγεί στον παρακάτω γραμμικό καθορισμό των ιδιομορφών στο Consteel.

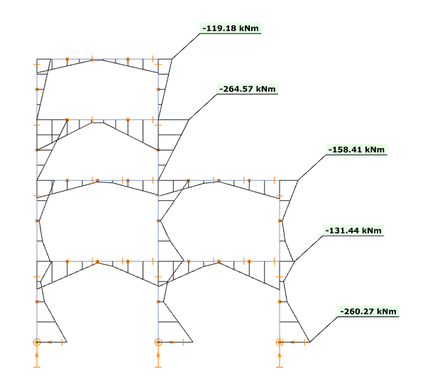
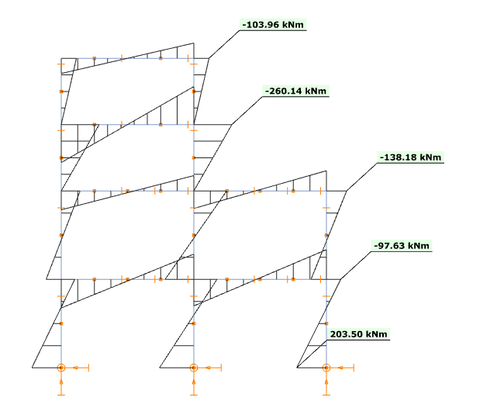
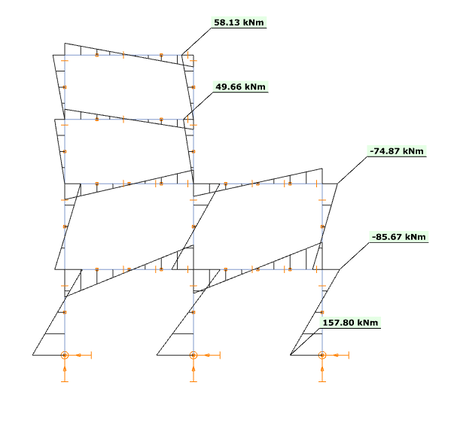
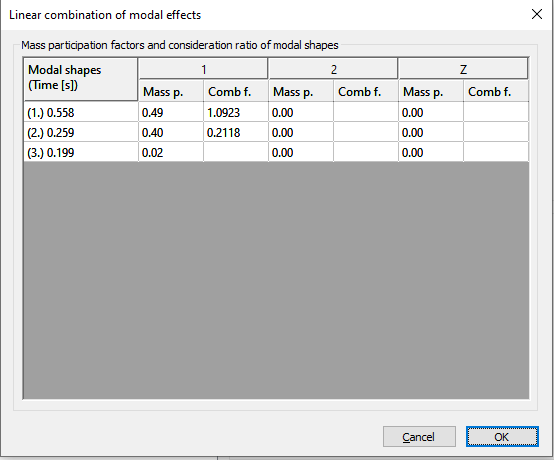
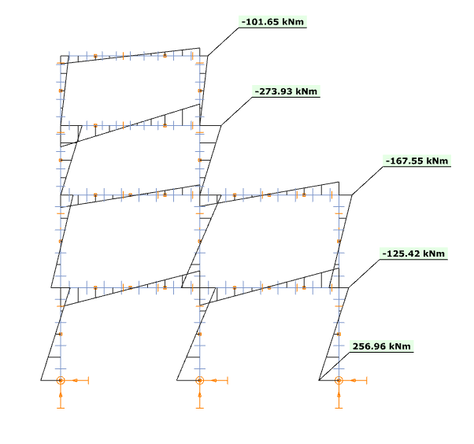
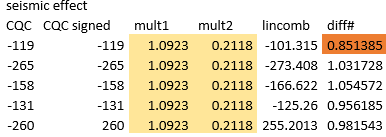
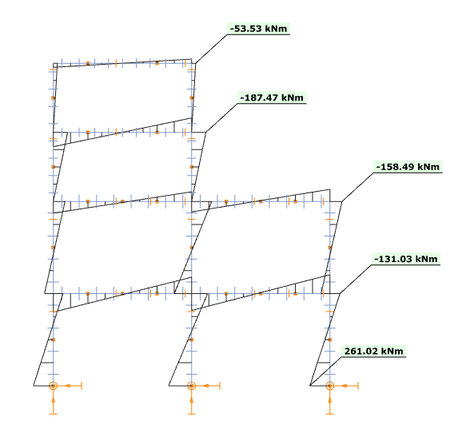
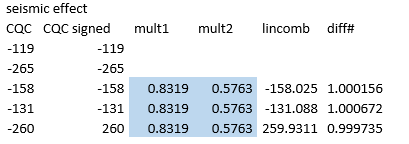
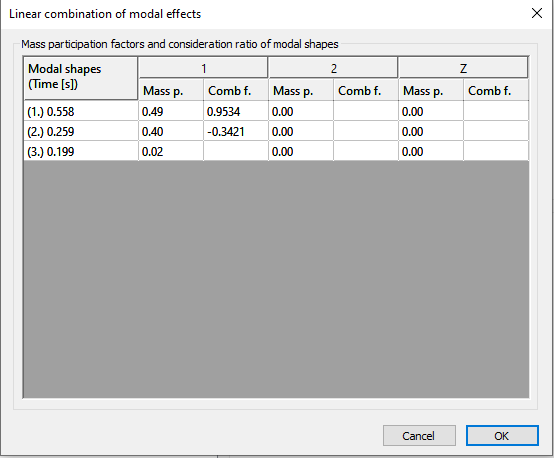
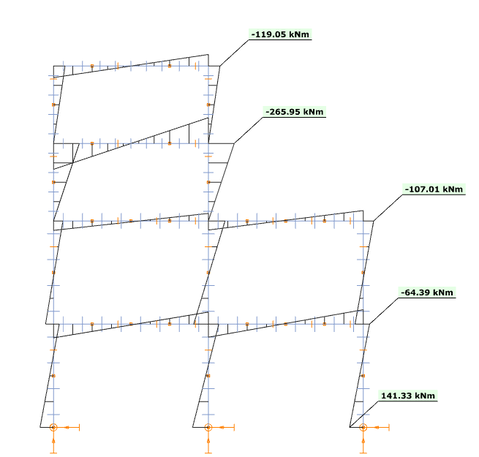
O γραμμικός συνδυασμών ιδιομορφών {1.0923 * [Modal forces]mode1 + 0.2118 * [Modal forces]mode2} παράγει τα παρακάτω αποτελέσματα ροπών κάμψης 

​​Τώρα φαίνεται ότι η προσέγγιση αυτή είναι πολύ καλύτερη σε σχέση με την εξέταση απλώς της πρώτης ιδιομορφής. Ειδικά για το πάνω μέρος της κατασκευής όμως έχει ως αποτέλεσμα χαμηλότερη ροπή κάμψης από την τιμή αναφοράς. Αυτό μπορεί να εξηγηθεί κοιτάζοντας το σχήμα του 2ου τρόπου ταλάντωσης: δημιουργεί ροπές κάμψης με διαφορετικό πρόσημο στο επάνω και κάτω μέρος της κατασκευής με έναν μόνο γραμμικό πολλαπλασιαστή και δεν μπορεί να ικανοποιήσει τις απαιτήσεις του κάτω και του άνω μέρους ταυτόχρονα. Φαίνεται λοιπόν ότι δικαιολογείται η δημιουργία γραμμικών συνδυασμών για το πάνω και το κάτω μέρος χωριστά. 

Βήμα 5
 Χρησιμοποιούνται 3 σημεία αναφοράς στο χαμηλότερο τμήμα της κατασκευής
A = [-138 -75; -98 -86; 203 158]
  -138   -75
   -98   -86
   203   158
b = [-158; -131; 260]
  -158
  -131
   260
x = [x1; x2]
>> lsqr(A,B)
όπου το lsqr συγκλίνει στην επανάληψη 2 σε μία λύση με σχετική τιμή υπολοίπου ίση με 0.00034
 
ans = 
    0.8319
    0.5763

​Υπάρχει εδώ μία τέλεια συμφωνία σε κάθε μία από τις 3 τιμές αναφοράς στο χαμηλότερο τμήμα.

Βήμα 6
Χρησιμοποιούνται 2 σημεία αναφοράς στο ανώτερο τμήμα της κατασκευής 
A = [-104 58; -260 50]
  -104    58
  -260    50
B = [-119; -265]
  -119
  -265
Καθώς ο αριθμός των εξισώσεων είναι ίσος με τον αριθμό των μη γνωστών πολλαπλασιαστών, αυτό το σύστημα μπορεί να επιλυθεί άμεσα.
ans =
     0.9534
   -0.3421

Υπάρχει τέλεια συμφωνία στα σημεία αναφοράς της άνω κατασκευής. Σημειώνεται ότι ο πολλαπλασιαστής για τη δεύτερη ιδιομορφή είναι αρνητικός. Αυτό εξηγεί γιατί δεν βρέθηκε ένας ενιαίος γραμμικός συνδυασμός για ολόκληρη την κατασκευή.

Βήμα 7
Το σεισμικό φαινόμενο έχει περιγραφεί με 2 γραμμικούς συνδυασμούς ιδιομορφών. Θα πρέπει να δημιουργηθούν λοιπόν 2 σετ σεισμικών συνδυασμών. Με τη βοήθεια των σετ δυνάμεων που προσδιορίζονται με βάση τους γραμμικούς συνδυασμούς ιδιομορφών, όλοι οι κρίσιμοι συνδυασμοί μπορούν να εκτελεστούν στο Consteel, χρησιμοποιώντας το ειδικό πεπερασμένο στοιχείο με 7 βαθμούς ελευθερίες. Αυτό περιλαμβάνει στατική ανάλυση πρώτης και δεύτερης τάξης, ανάλυση γραμμικού λυγισμού.
Τα αποτελέσματα της ανάλυσης πρώτης και δεύτερης τάξης καταλήγουν σε ροπές κάμψης σε ισορροπία, κατάλληλες για τον σχεδιασμό και των συνδέσεων.
Με τη βοήθεια των αποτελεσμάτων γραμμικού λυγισμού με τα πεπερασμένα στοιχεία 7DOF (7 βαθμών ελευθερίας), είναι διαθέσιμες όλες οι σχετικές μορφές λυγισμού για την εκτέλεση ανάλυσης λυγισμού χρησιμοποιώντας τη Γενική Μέθοδο που ορίζεται στον Ευρωκώδικα 3.
 
Συμπέρασμα 
Η παρουσιαζόμενη μέθοδος παρείχε μια πρακτική δυνατότητα καθορισμού κατάλληλων γραμμικών συνδυασμών των ιδιομορφών, οι οποίοι μπορούν να χρησιμοποιηθούν ως εναλλακτική λύση στους τετραγωνικούς συνδυασμούς των ιδιομορφών που προβλέπονται στους ευρωκώδικες. Χρησιμοποιώντας τα γραμμικά αθροίσματα των ιδιομορφών, είναι δυνατοί όλοι οι έλεγχοι που απαιτούνται σε στατικές μελέτες μεταλλικών κατασκευών ειδικά όσον αφορά στους ελέγχους για τις σεισμικές δράσεις.