Ο ευρωκώδικας EN 1993-1-3 περιλαμβάνει 3 "μυστικούς" τύπους για μεταλλικές διατομές ψυχρής έλασης7/1/2019
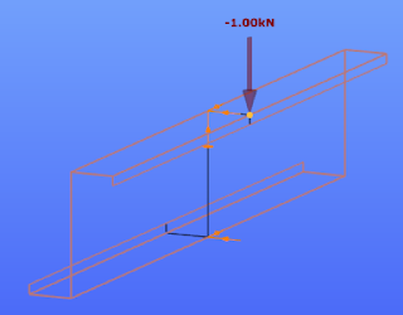
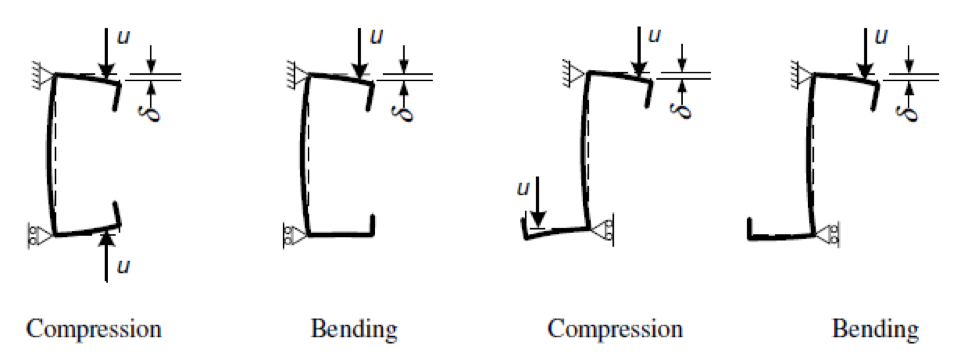
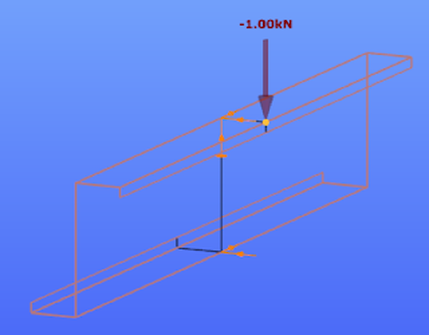
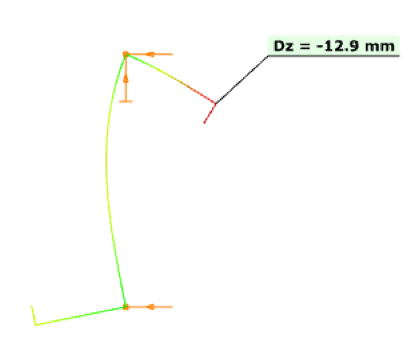
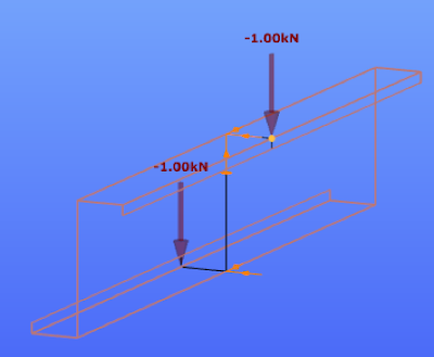
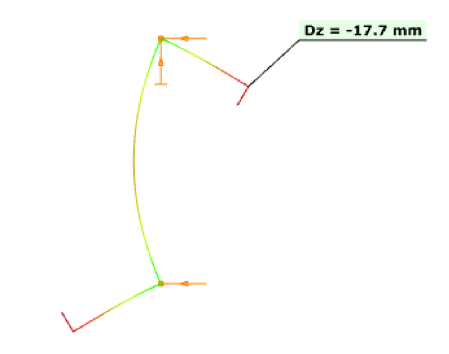
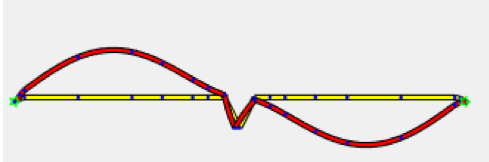
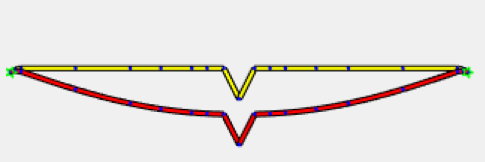
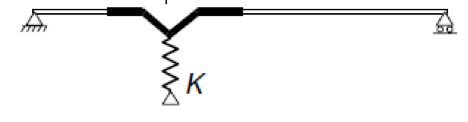
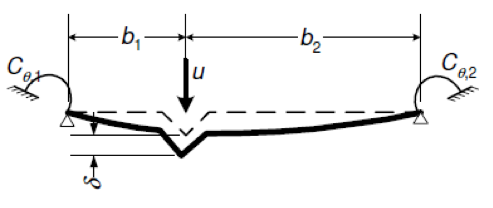
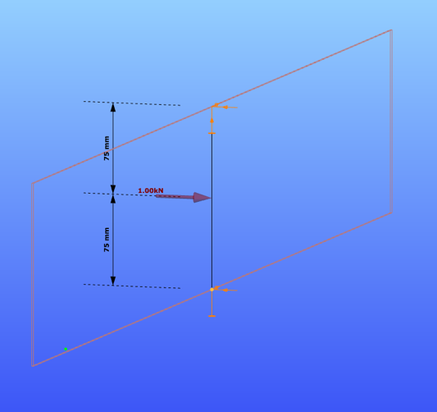
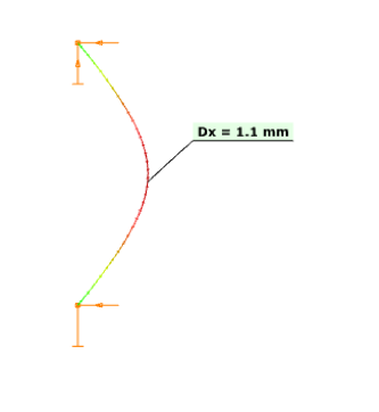
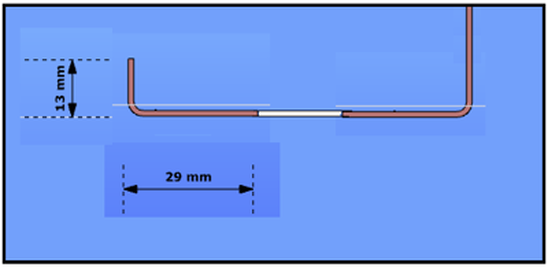
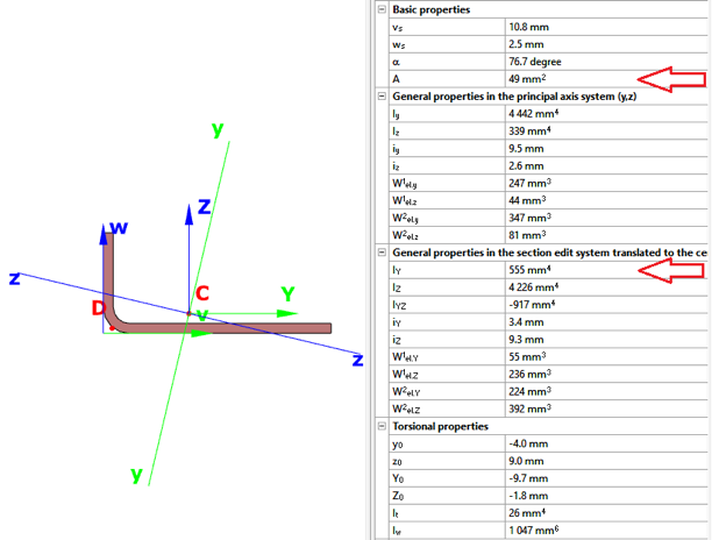
Οι τρεις αυτοί τύποι είναι οι παρακάτω: Ο πρώτος τύπος (5.10) χρησιμοποιείται όταν ελέγχεται η ικανότητα μιας πλευρικής ενίσχυσης στο να σταθεροποιήσει ένα θλιβόμενο πέλμα μιας διατομής Z ή C. Κατά την διάρκεια του στρεβλωτικού λυγισμού το ενδιάμεσο σημείο του πέλματος με το lip (θεωρείται πλευρική ενίσχυση) αναμένεται να μετακινηθεί σε μία διεύθυνση κάθετη στο πέλμα. Ο τύπος αυτός δίνει την τιμή δυσκαμψίας που παρέχεται από μία διατομή Z ή C, όταν θεωρείται ότι κατά την διάρκεια των παραμορφώσεων το σημείο της τομής του πέλματος με τον κορμό δεν μετακινείται. Αυτό πρακτικά αντιστοιχεί στην εισαγωγή στηρίξεων στους σχετικούς κόμβους όπως εμφανίζεται στην εικόνα 5.6 του EN 1993-1-3. Όταν μία θλιβόμενη πλευρική ενίσχυση πάει να λυγίσει, τότε θα παρεμποδιστεί μερικώς η παραμόρφωσή της στους κόμβους στους οποίους συνδέεται με την υπόλοιπη διατομή. Ανάλογα με την κατανομή των ορθών τάσεων στην διατομή, μία ή δύο πλευρικές ενισχύσεις μπορεί να βρίσκονται υπό θλίψη. Αν και οι δύο ενισχύσεις βρίσκονται υπό θλίψη και τείνουν να λυγίσουν, τότε η ικανότητα της διατομής να παρεμποδίσει το λυγισμό θα πρέπει να μοιραστεί μεταξύ αυτών. Αυτή απαιτούμενη μοιρασιά αντιπροσωπεύεται από τον συντελεστή kf. Η τιμή της ελαστικής δυσκαμψίας χρησιμοποιείται ως κατανεμημένη ελαστική στήριξη στον υπολογισμό της αντίστασης σε λυγισμό τς πλευρικής ενίσχυσης. Οι τιμές της δυσκαμψίας τυπικά υπολογίζονται ως ο λόγος των παραμορφώσεων που προκαλούνται από την εφαρμογή ενός μοναδιαίου φορτίου. Στην περίπτωση αυτή τα μοναδιαία φορτία εφαρμόζονται παράλληλα στην αναμενόμενη μετακίνηση των θλιβόμενων πλευρικών ενισχύσεων. Στο παρακάτω μοντέλο του ConSteel (Κατεβάστε το μοντέλο από εδώ) αναπαράγεται ο υπολογισμός της δυσκαμψίας για μία διατομή μορφής Zήτα με μήκος 1m (ως απλούστευση τα μοναδιαία φορτία τοποθετήθηκαν στο σημείο τομής του πέλματος με την ακραία ενίσχυση (lip) και όχι στον κεντροβαρικό άξονα της πλευρικής ζώνης): Z τεγίδα, ονοματικό πάχος=1.30 mm, 200 mm ύψος, 72 mm πλάτος σε συμμετρικά πέλματα, 15.5 mm ύψος των lips Στην περίπτωση της κάμψης My: kf = 0, b1 = b2 = 72 mm, hw = 198.7 mm, t = 1.26 mm K1 = 210000*1.26^3/4*(1-0.3^2)*1/(72^2*198.7+72^3+0.5*72*72*198.7*1.0) = 0.08 N/mm2 Προκύπτει κατακόρυφη μετακίνηση από το σημειακό φορτίο ίση με 12.9 mm. Η τιμή της ελαστικής δυσκαμψίας είναι: K = u / δ=1 kN/m / 12.9 mm = 0.0775 N/mm2 χωρίς την επίδραση από την εγκάρσια καταπόνηση. Πολλαπλασιάζοντας αυτή την τιμή με (1-ν2) προκύπτει 0.0775/(1-0.32) από όπου λαμβάνουμε τελικά την τιμή 0.08 N/mm2 Στην περίπτωση της θλίψης: kf = 1.0, b1 = 72 mm, hw = 198.7 mm, t = 1.26 mm K1 = 210000*1.26^3/4*(1-0.3^2)*1/(72^2*198.7+72^3+0.5*72*72*198.7*1.0) = 0.06 N/mm2 Προκύπτει κατακόρυφη μετακίνηση από το σημειακό φορτίο ίση με 17.7 mm. Η τιμή της ελαστικής δυσκαμψίας είναι: K = u / δ=1 kN/m / 17.7 mm = 0.056 N/mm2 χωρίς την επίδραση από την εγκάρσια καταπόνηση. Πολλαπλασιάζοντας αυτή την τιμή με (1-ν2) προκύπτει 0.056/(1-0.32) από όπου λαμβάνουμε τελικά την τιμή 0.06 N/mm2 Συνεχίζουμε με τον δεύτερο "μυστικό" τύπο: Ο τύπος αυτός (5.11) χρησιμοποιείται όταν ελέγχεται η ικανότητα μιας ενδιάμεσης ενίσχυσης να σταθεροποιήσει ένα θλιβόμενο έλασμα κορμού. Όταν η ενδιάμεση ενίσχυση είναι αρκετή δύσκαμπτη, τέμνει το μακρύτερο έλασμα του κορμού σε μικρότερα τμήματα. Κατά την διάρκεια του λυγισμού μία δύσκαμπτη ενίσχυση δεν θα μετακινηθεί, οπότε το έλασμα θα στρίψει μεταξύ των δύο άκρων (έχουμε την σταθεροποίηση από τα πέλματα) και της ενίσχυσης: Αν η ενίσχυση δεν είναι αρκετά δύσκαμπτη, ήδη σε αρκετά χαμηλότερο επίπεδο έντασης θα εμφανιστεί λυγισμός λόγω στρέβλωσης ο οποίος χαρακτηρίζεται από μία μετακίνηση της ενίσχυσης και από τον λυγισμό του ελάσματος του κορμού με το μισό κύμα να είναι ίσο με το μήκος του ελάσματος: Σε μία τέτοια περίπτωση ο Ευρωκώδικας επιτρέπει ακόμα ότι ο λυγισμός του ελάσματος του κορμού θα συμβεί μεταξύ των άκρων και των ενδιάμεσων ενισχύσεων, αλλά μειώνει το πάχος των ζωνών των ενδιάμεσων ενισχύσεων, με σκοπό να αντισταθμιστεί για δυσκαμψία μικρότερη από την ιδεατή. Αυτό το αντιστάθμισμα θα εξαρτάται από την αντίσταση σε λυγισμό της ενίσχυσης όταν υπόκειται σε θλίψη. Το απλοποιημένο μοντέλο που χρησιμοποιείται στην διαδικασία αυτή από τον Ευρωκωδίκα εμφανίζεται παρακάτω. Ως απλούστευση θεωρείται ότι το έλασμα του κορμού συνδέεται με την υπόλοιπη διατομή με αρθρώσεις. Αυτό σημαίνει ότι η μορφή λυγισμού του δεν επηρεάζεται από την ενίσχυση των συνδεδεμένων τμημάτων και ότι τα άκρα τους μπορούν να περιστραφούν ελεύθερα. Τα άκρα του ελάσματος στηρίζονται και το έλασμα μπορεί και παρέχει μία ελαστική στρώση στην ενίσχυση, η οποία θα ληφθεί υπόψη ως "βοήθεια" στον υπολογισμό της αντίστασης σε λυγισμό. Αυτή η στρώση (bedding) αναπαριστάται από την ελαστική δυσκαμψία K: Η τιμή του ελατηρίου η οποία αναπαριστά σε αυτό το μοντέλο την στρώση (bedding) η οποία παρέχεται από το έλασμα, υπολογίζεται ως ο λόγος της μετακίνησης που που επιτυγχάνεται από την εφαρμογή ενός μοναδιαίου φορτίου στο κέντρο βάρους της ενίσχυσης. Στην περίπτωση αυτή το μοναδιαίο φορτίο εφαρμόζεται κάθετα στο έλασμα του κορμού. Ο τύπος (5.11) δίνει την βύθιση (δ) από ένα τέτοιο μοναδιαίο φορτίο (u). Στο παρακάτω μοντέλο του ConSteel (κατεβάστε το από εδώ) αναπαράγεται ο υπολογισμός της δυσκαμψίας του ελάσματος κορμού για μία διατομή μορφής C με μήκος 1m, όπου ο κορμός έχει ενισχυθεί μέσω μιας διαμήκους ενδιάμεσης ενίσχυσης κορμού. Καθώς ο τύπος (5.11) δίνει την βύθιση από ένα συγκεντρωμένο φορτίο, η ενδιάμεση ενίσχυση μορφής "V" δεν θα μοντελοποιηθεί, παρά μόνο τα επίπεδα ελάσματα με πάχος. C διατομή, ονομαστικό πάχος = 1.524 mm, 150 mm ύψος με μία ενδιάμεση ενίσχυση 8 mm depth η οποία βρίσκεται στο μέσο του ελάσματος Στην περίπτωση που εφαρμόζεται αξονική θλιπτική δύναμη στην διατομή τότε: δ= 1*75^2*75^2/(3*(75+75))*12*(1-0.3^2)/(210000*1.524^2) = 1.033 mm Από τα παραπάνω προκύπτει οριζόντια μετακίνηση από το σημειακό φορτίο ίση με 1.135 mm χωρίς την επίδραση της εγκάρσιας καταπόνησης. Πολλαπλασιάζονται αυτή την τιμή με (1-ν2) παίρνουμε 1.135 *(1-0.32) = 1.033 mm Αυτή η μετακίνηση θα μετατραπεί σε Κ τιμή ελαστικής δυσκαμψίας (spring). με αποτέλεσμα K = u/δ=1/1.033 = 0.968 N/mm2 Στο σημείο αυτό, θα δείξουμε πώς υπολογίζεται η αντίσταση σε λυγισμό της ενίσχυσης. Για τον υπολογισμό αυτό χρειάζεται να λάβουμε υπόψη τις τιμές για τα ελατήρια. Μέχρι τώρα, έχουμε δείξει πώς υπολογίζεται η ελαστική δυσκαμψία „K” για την πλευρική και την ενδιάμεση ενίσχυση. Τώρα θα δείξουμε πώς μπορούμε να προχωρήσουμε παραπέρα. Ο στόχος είναι να προσδιοριστεί πόσο αποδοτικά μπορεί αυτή η ενίσχυση να στηρίξει τα συνδεδεμένα θλιβόμενα ελάσματα. Για να ληφθεί υπόψη ο τοπικός λυγισμός του θλιβόμενου ελάσματος θα υπολογιστούν το ενεργά πλάτη. Αυτά τα πλάτη μπορούν είτε να υπολογιστούν για ένα έλασμα στηριζόμενο στα δύο άκρα είτε για ένα έλασμα στηριζόμενο σε ένα άκρο μόνο, με την χρήση του πίνακα 4.1 και 4.2, αντίστοιχα. Αν μία ενίσχυση πληροί τις ελάχιστες κατασκευαστικές απαιτήσεις, θα υποθέσουμε αρχικά ότι είναι αρκετά άκαμπτη ώστε να δράσει ως στήριξη. Με βάση αυτή την υπόθεση θα βρούμε τα ενεργά μήκη των συνδεδεμένων θλιβόμενων ελασμάτων, θεωρώντας επίσης ότι εντείνονται λόγω φορτίων μέχρι το όριο διαρροής. Από τη στιγμή που γνωρίζουμε τα ενεργά πλάτη των τμημάτων των ελασμάτων που συνδέονται με την ενίσχυση, γνωρίζουμε επίσης το φορτίο για το οποίο υποτίθεται η ενίσχυση θα μπορεί αναλάβει χωρίς να εμφανίσει λυγισμό, ώστε να επαληθεύσουμε την πρώτη υπόθεση. Επομένως, στη συνέχεια υπολογίζουμε την αντίσταση σε καμπτικό λυγισμό της ενίσχυσης. Αν βρούμε ότι είναι μικρότερη από ότι στην αρχή θεωρήθηκε, επιστρέφουμε στο πρώτο βήμα, πηγαίνοντας χαμηλότερα από την ένταση η οποία πρέπει να είναι ίση με την επιτυγχανόμενη αντίσταση σε λυγισμό της ενίσχυσης (λυγισμός λόγω στρέβλωσης). Αυτό το χαμηλότερο επίπεδο έντασης μπορεί πράγματι να έχει ως αποτέλεσμα διαφορετικά ενεργά πλάτη. Μέσω μιας επαναληπτικής διαδικασίας μπορούμε να φτάσουμε στο επιθυμητό αποτέλεσμα. Μετά την ολοκλήρωση, ο υπολογισμός της τιμής της τελικής αντίστασης έναντι λυγισμού της ενίσχυσης, ενσωματώνεται σε ένα ισοδύναμο ενεργό πάχος το οποίο εφαρμόζεται στην ενίσχυση και στα συνδεδεμένα ενεργά τμήματα του ελάσματος. Στην ως άνω αναφερόμενη επαναληπτική διαδικασία, η τιμή „K” της ενίσχυσης θα χρειαστεί για να προσδιοριστεί η αντίσταση σε καμπτικό λυγισμό της ενίσχυσης. Αυτή η αντίσταση θα υπολογιστεί με την βοήθεια ενός μοντέλου μιας απλής δοκού, όπου η σταθεροποίηση που παρέχεται από τα εναπομείναντα τμήματα της διατομής χρησιμοποιείται ως μία συνεχής στρώση (bedding) του „K”. Η διατομή της δοκού αντιστοιχεί στην ενίσχυση και στα συνδεόμενα τμήματα του ελάσματος και υπόκειται στο τρέχον επίπεδο έντασης κάθε φορά στην επαναληπτική διαδικασία, θεωρώντας μία απλούστευση με σκοπό να υπάρχει συνέχεια κατά μήκος. Το μήκος της δοκού στο μοντέλο αυτό είναι άγνωστο προς το παρόν, και χρειάζεται να να είναι ίσο με το μισό του μήκους κύματος της μορφής λυγισμού η οποία αναμένεται να είναι περίπου 1.5-3 φορές το ύψος της εξεταζόμενης διατομής ψυχρής έλασης. O λυγισμός λόγω στρέβλωσης θα εμφανιστεί μόνο αν το μήκος της ενίσχυσης είναι σημαντικά μεγαλύτερο από αυτό το τυπικό μήκος. Ως μία περαιτέρω απλούστευση ο Ευρωκώδικας προτείνει ένα άπειρο μήκος ως την δυσμενέστερη περίπτωση, επειδή σε αυτή την περίπτωση υπάρχει μία αναλυτική λύση στην βιβλιογραφία: Σε αυτό τον τύπο το „K” είναι η τιμή του ελατηρίου και αντιπροσωπεύει την ελαστική τιμή της ενίσχυσης την οποία η εναπομένουσα διατομή μπορεί να παρέχει στην ενίσχυση. Έχουμε επίσης τις ιδιότητες της διατομής της αντίστοιχης ενίσχυσης μαζί με τα συνδεδεμένα ενεργά πλάτη των στηριζόμενων ελασμάτων, την ονομαστική περιοχή και την αδράνεια περί κάθετο άξονα στην αναμενόμενη διεύθυνση λυγισμού της ενίσχυσης ενώ Ε είναι το μέτρο ελαστικότητας με βάση το υλικό του χάλυβα. Ο τύπος αυτός δίνει το επίπεδο ελαστικής τάσης όπου εμφανίζεται ο ελαστικός λυγισμός. Από τη στιγμή που αυτό πραγματοποιείται, υπολογίζεται η μειωμένη λυγηρότητα και επιτυγχάνεται η αντίσταση σε στρεβλωτικό λυγισμό με την χρήση των ειδικών καμπύλων λυγισμού σύμφωνα με τους τύπους (5.12a-c) του EN 1993-1-3. Η καταλληλότητα του τύπου (5.15) μπορεί εύκολα να παρουσιαστεί μέσω ενός απλού μοντέλου του ConSteel. Ας υποθέσουμε ότι έχουμε μία διατομή μορφής Z η οποία έχει αναφερθεί νωρίτερα, και η οποία υπόκειται σε θλιπτική δύναμη. Παράλληλα ας υποθέσουμε ότι έχουμε ήδη υπολογίσει τις τιμές του ενεργού πάχους. Η αντοχή διαρροής του υλικού είναι 235 MPa και το πάχος της επίστρωσης είναι 0.04 mm. Στη συνέχεια βρίσκουμε ότι το ενεργό πάχος της ακραίας ενίσχυσης (lip) και του πέλματος είναι αντίστοιχα ceff=13 mm και beff=29 mm. Οι ιδιότητες της διατομής μπορούν να υπολογιστούν από το ConSteel Στην αρχή αυτού του άρθρου αναφέρθηκε μία τιμή του „K” ίση με K1=0.080 N/mm2 για την πλευρική ενίσχυση. Χρησιμοποιώντας τις τιμές αυτές όπως υπολογίζονται από τον αλγόριθμο του ConSteel για τις διατομές (section module) η κρίσιμη τάση θα είναι:
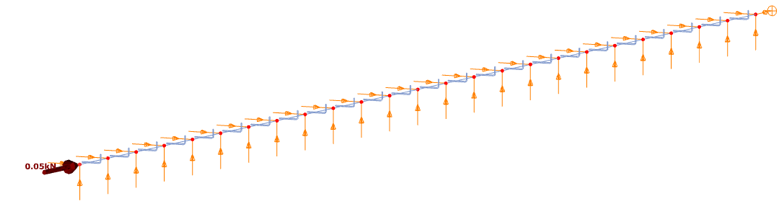
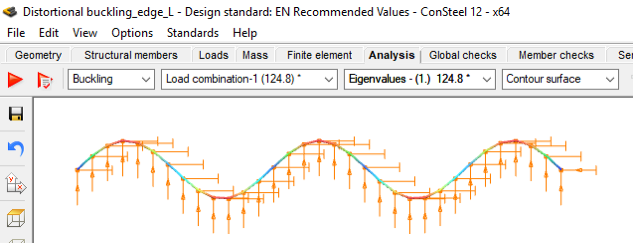
σcr= 2*sqrt(K*E*Is)/As = 2*sqrt(0.080 * 210000 * 555)/49 = 124.63 MPa Με σκοπό να δημιουργηθεί ένα μοντέλο στο ConSteel και να παρουσιαστεί αυτός ο υπολογισμός ας υποθέσουμε ότι έχουμε ένα αυθαίρετο μήκος μοντέλου 3000 mm το οποίο φαίνεται ότι είναι ικανό να προκαλέσει στρεβλωτικό λυγισμό (καμπτικό λυγισμό σε αυτή την περίπτωση). Μία κατακόρυφη συνεχή στρώση (bedding) των 0.08 N/mm/mm έχει εφαρμοστεί καθώς και μία θλιπτική δύναμη NEd=49*1=49 N αντίστοιχη με την μοναδιαία θλιπτική τάση του 1 MPa.
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
ERGOCADΝέα και ενδιαφέροντα άρθρα, tips, events κ.α. ΑΡΧΕΙΟ
May 2024
ΚΑΤΗΓΟΡΙΕΣ
All
|


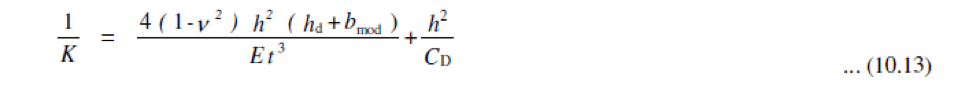




 RSS Feed
RSS Feed